Тугие косы
«Знания – всем», научно-популярный альманах, № 6, 1951, Новосибирск, с. 23-25, напечатано по книге В. Полозова «Занимательно о физикѣ», С.-Петербургъ, 1908 [1]
О маятнике и долженствующей походке юных барышень
Виктор Полозов
Наверняка почти каждому из читателей доводилось хоть однажды наблюдать следующую картину. Впереди вас идёт юная особа с туго заплетённой косой или с двумя косами. Какое-то время они пребывают, можно сказать, что в покое, лишь слегка намекая на покачивания в такт шагов своей хозяйки. Потом их раскачивание становится очевидным, и в какой-то момент они пускаются в форменную свистопляску с неимоверной амплитудой, не теряя синхронности с шагами. Причём, шаг обладательницы сей красоты не меняется ни в скорости, ни в широте. Кто-то из вас, вероятно, отмечал явную характерность этого явления и совсем уже некоторые задавались вопросом о его происхождении. Попробуем в нём разобраться.
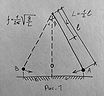
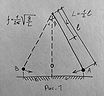
Начнём с очевидного – раскачивающиеся косы можно представить в виде маятника. Для простоты ограничимся одной, (рис.1).
Рисунок фиксирует момент колебаний близких к равновеликим. Одно полное колебание нашего маятника есть его перемещение из точки А в точку В и обратно. Частота колебаний определяется их числом в единицу времени – в секунду (прим. редакции: в отличие от оригинального издания, измерения всех величин приведены здесь к действующим на настоящий момент международным). В нашем случае, одно полное колебание соответствует двум шагам – ведь именно шаги и есть те импульсы, что раскачивают наш «маятник». Что ж, самые прозорливые из читателей уже наверняка вспомнили об уже известном нам понятии резонанса, который и явится наиболее вероятным объяснением описанного фривольного поведения кос. Итак – гипотеза: частота шагов наших барышень оказывалась близкой к резонансной частоте их «маятниковых» кос. Проверим это расчётами.
Формула резонансной частоты маятника следующая:
f = (1/2π) √(g/L), Гц
где L – длина от точки подвешивания маятника до центра его масс, м
g – ускорение свободного падения, м/с ²
Мы не можем оперировать фактической длиной косы, для расчётов нам необходимо наш маятник физический привести к математическому, отсюда и появляется приведённая длина. В нашем случае справедливо полагать, что масса распределена по косе примерно одинаково, и, пренебрегая незначительным сужением в конце последней, принимаем, что приведённая длина L равна половине фактической длины косы l.
Опираясь на весь наш практический опыт, включая экстремальные случаи, ограничим диапазон фактической длины косы двадцати пятью и ста сантиметрами. Выбрав внутри диапазона опорные точки, получаем следующие результаты:
фактическая длина косы, l / приведённая длина, L / резонансная частота, f
25 см / 12.5 см/ 1.4 Гц
45 см / 22.5 см / 1.05 Гц
50 см / 25 см / 0.998 Гц
60 см / 30 см / 0.9 Гц
70 см / 35 см / 0.84 Гц
100 см / 50 см / 0.7 Гц
Рассмотрим получившееся. Отбросив крайние точки – 25 и 100 см – мы видим, что резонансная частота крайне близка к значению «два шага в секунду». А это, признаем, соответствует обычной скорости движения для случая целевого перемещения из одного пункта в другой (мы не рассматриваем здесь «бесцельное блуждание» или, наоборот, «бег», побуждаемый вынужденными обстоятельствами). Да и крайние точки, по существу, несильно отличаются со своими двумя шагами за чуть менее полутора секунд для ста сантиметровой и за около 0.7 секунд для 25-ти сантиметровой косы.
Таким образом мы видим, что практически в любой ситуации непринуждённого пешего движения, при любой длине косы, её обладательница подвержена попаданию в описанный резонанс, привлекая к себе тем самым повышенное внимание противоположного пола. Мы не берём на себя здесь функции блюстителей нравов, тем более, наблюдая некоторые их неизбежные изменения, а можем лишь обозначить способ избежать такового, если угодно, конфуза. Походка юной барышни должна быть максимально отлична от оной сошедшего на берег матроса, привыкшего к раскачивающейся палубе под ногами.
[1] Полозовъ, Викторъ. «Занимательно о физикѣ», С.-Петербургъ, 1908, популяризаторское изданіе, рекомендованное Министерствомъ народнаго просвѣщенія въ качествѣ дополнительной литературы для училищъ и гимназій Россійской имперіи
Игорь Савченко
Минск, декабрь 2020


















-thumb.jpg?alt=media&token=5e9ae36a-a7ea-44cd-8765-81a253749759)
-thumb.jpg?alt=media&token=75e9a684-08cb-4915-8abf-b523c9c127ea)


ruhi-i-mizhnarodny-pospeh_-vyniki-goda-%D1%9E-mastactve-%E2%80%94-reform.by-thumb.jpg?alt=media&token=4644da18-2e31-44ff-b733-10da53b0a833)