Мнимая угроза

Труды РЭНД Корпорэйшн по теории игр, RAND Corporation Papers on Game Theory, Santa Monica, California, Volume II, 1951, pp. 19-23

К вопросу о противоборствующих стратегиях независимых игроков

Амром Кинсли

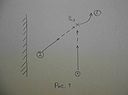
Обратимся к рисунку. По мостовой, вдоль длинной кирпичной стены дома двигается прохожий (1). Находящийся между ним и стеной голубь (2) (пребывавший там в поисках подножного корма) воспринимает приближающегося человека, как надвигающуюся угрозу, и пытается её избежать.

Не будучи в состоянии адекватно оценить ситуацию, голубь изначально прибегает к ошибочной тактике и, намереваясь вырваться из охвата, устремляется по мостовой пересекающимся с прохожим курсом. Ощущение фатального неравенства усилий и нарастающая паника лишает птицу и без того малых шансов радикально переменить направление своего движения на действительно верное. В последние мгновения – из-под самых башмаков «агрессора» – сизарь спасается бегством по воздуху, оставляя победителю кормовую территорию, но сохранив главное – жизнь.

Пренебрегши той малостью, что вся «схватка» осталась совершенно вне внимания погружённого в свои мысли прохожего, мы воочию получим картину успешно реализованной им стратегии «мнимой угрозы» по Гёльвицу [1], состоящей в том, чтобы убедить противника в якобы действительности своих агрессивных намерений и с малыми затратами побудить его к желаемым для себя шагам. Уязвимость стратегий этого класса, когда истинность намерений камуфлируется предпринимаемыми действиями, обоюдная (ведь голубь, на самом деле, мог лишь инсценировать своё поведение дабы усыпить бдительность более сильного противника и коварно его заманить в уготовленную ловушку). Чем дольше противникам будет удаваться держать друг друга в неведении относительно своих интересов, тем выше шансы каждого на победу. Но всегда неизбежно наступает момент, когда скрывать свои истинные намерения более невозможно. Момент этот определяется именно логикой развития избранной стратегии – с одной это происходит раньше, с другой – позже. Таким образом, искусство игрока заключается в выборе плана действий, который был бы не только более изощрённым сам по себе, но и позволял бы скрывать себя дольше, чем это же будет удаваться противнику. Недостаточный прогресс в теоретических разработках таковых ситуаций объясняется, в том числе, и неразвитостью терминологии. Даже в этом тексте мы пока были вынуждены прибегать преимущественно к способам описательным. Попробуем это исправить.

Постулат [Кинсли, прим. пер.]: у каждой стратегии есть, как минимум, один признак, присущий ей и только ей, и этот признак определяет существо этой стратегии – является сущностным и называется принципом стратегии. Количество таких сущностных признаков у стратегии определяет её кратность N.

Допущение [Кинсли, прим. пер.]: для двух изолированных (*) противников всегда существуют два непересекающихся множества стратегий, где одно (А) содержит стратегии, обеспечивающие победу над стратегиями, принадлежащими другому множеству (Б). Принадлежность стратегии тому или иному множеству определяется принадлежностью какому либо из множеств её принципа.

Следствие первое: для двух изолированных противников с однократными стратегиями: если стратегия одного из них принадлежит множеству Б, то для победы другого достаточно (но не необходимо), чтобы его стратегия принадлежала множеству А.

Следствие второе: для двух изолированных противников с многократными стратегиями: если N принципов стратегии одного из них принадлежит множеству Б, то для победы другого достаточно (но не необходимо), чтобы как минимум N+1 принципов его стратегии принадлежало множеству А.

Успех, таким образом, зависит от того, насколько быстро кто-либо из игроков разгадает применяемую стратегию другого, соотнеся её со множеством Б, дабы успеть принять в ответ адекватную эффективную противоборствующую стратегию из множества А.

Аксиома о пределе принципа [Кинсли, прим. пер.]: сколь долго бы игрок не старался сокрыть признаки применяемой им стратегии, всегда наступает момент времени tх, после которого сокрытие принципа этой стратегии становится невозможным. Протяжённость временного отрезка, в течение которого удаётся скрывать принцип применяемой стратегии, называется пределом данного принципа у данного игрока в определённом противостоянии с другим игроком.

Величина предела принципа для любых конкретных условий имеет две составляющие: объективную и субъективную. Первая, при прочих равных условиях, определяется исключительно свойствами применяемой стратегии, как таковой. Вторая зависит от умелости применения данным игроком этой стратегии в заданных условиях.

Следствие третье: Если выявленные принципы однократных стратегий обоих игроков оказываются в одном и том же множестве – А или Б – то какая-то доля вероятности выигрыша каждого игрока прямопропорциональна величине предела принципа его стратегии, другая же доля вероятности выигрыша зависит от соотнесения классов эффективности каждой из выявленных стратегий.

Возростание числа противоборствующих игроков, при сохранении их статуса изолированности (незаключение союзов), принципиально картину не меняет, а лишь удлиняет цепочку сравнений и соотнесений.

(*) прим. пер.: изолированный игрок – игрок, не имеющий союзников и действующий самостоятельно, исключительно в соответствии с собственными интересами

[1] Goelwitz, Dietrich. Strategie der modernen Kriegsführung, Militärwissenschaftliche Rundschau, XI-1937, Berlin, S. 44-58

Игорь Савченко

Минск, июль 2015