Белый автомобиль
Труды по теории вычислительных систем Швейцарской высшей технической школы Цюриха, ETHZ Proceedings on Computer Systems, Eidgenössische Technische Hochschule Zürich, Vol. 28, 1954, pp. 48-51
О существе вероятностных связей
Макс Флеге
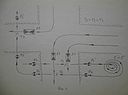
Воспользуюсь небольшим происшествием, случившимся с одним из моих коллег. В какой-то из дней, ближе к вечеру, у него была назначена встреча с одной молодой особой, приятной во всех отношениях. Время ещё оставалось, и он решил заполнить его неким необязательным, не раз отсроченным уже делом – вроде визита к часовщику. Путь знакомого моего пролегал через перекрёсток (рис.1).
Последним из автомобилей, пропущенных им, прежде чем пересечь дорогу (Р1), оказался большой белый мерседес (А1), на который нельзя было не обратить внимания. Проведя некоторое время у часовщика (t’ – t”), коллега вернулся к перекрёстку (Р2). Пропустив машины, он заметил, что последним в их веренице снова оказался большой белый мерседес, но с другим номерным знаком (А2). Недоброе шевельнулось у него в груди – безотчётно он решил, что выпадение такого приметного события дважды в одном месте и за короткое время снижает его шансы на назначенную встречу. Ему предстояла ещё одна часть того перекрёстка. Надо ли описывать, с какими чувствами подходил он к краю тротуара (Р3), а главное, что ощутил, когда почти ожидаемо заметил большую белую машину, опять мерседес (А3) – последнюю из тех, что ему следовало пропустить вперёд себя. Почти обречённо добрёл он до места встречи, – его визави так и не явилась, сколь он её ни ждал.
Попробуем теперь, насколько возможно, абстрагировать ситуацию и станем оперировать привычными нам категориями. Положим, что для любого произвольного события А найдётся, по крайней мере, одно событие Б, вероятность свершения которого прямо либо обратно пропорциональна вероятности свершения события А. Такие пары событий А и Б будем называть вероятностно зависимыми. Принято полагать, что наша осведомлённость, равно как и неосведомлённость, о том, в чём же именно состоит событие Б, соответствующее известному событию А, никак не влияет на вероятность свершения этого самого события Б. Предположим теперь существование миров, где таковой постулат не действует, и степень нашего знания (равно и незнания) о существе события Б способно влиять на вероятность его свершения.
Иными словами, такой мир способен замечать и реагировать на нашу осведомлённость. Следующим шагом на этом пути станет признание нашего произвола в целеполагании, т.е. возможности для нас и нашей же способности назначать известному событию А его вероятностно зависимую (в плюс либо минус) пару – событие Б. И мир примет такое назначение, и станет на него реагировать. Будем ли мы непременно осведомлены о характере таковой реакции – вопрос.
Равно вопросом является и следующее – по каким признакам можем мы различить мир равнодушный к нашему знанию события Б и мир, это знание учитывающий. Незыблемы ли с ходом времени отличительные характеристики таковых миров, может ли один трансформироваться в другой и наоборот? Всегда ли обоснованы наши представления о тех или иных известных механизмах, казалось бы, столь привычного и обустроенного «нашего» мира?
И, наконец – так не без участия ли моего приятеля события приняли именно тот оборот, которого он столь опасался?
Игорь Савченко
Минск, май 2017